MÓDULO II MATEMÁTICAS
- 1. Competencias y Criterios
- 2. Funciones Trigonométricas, circunferencia y parábola, probabilidad con conteo y probabilidad condicional
- 2.1. Funciones Trigonométricas
- 2.1 – Construcción de la tabla de valores
- 2.1 – Análisis de la tabla de valores
- 2.1.1. – Actividad 01
- 2.2. Análisis de gráficas
- 2.2. – Traslaciones de funciones
- 2.2. – Reflexión de funciones
- 2.2. – Compresión y alargamiento
- 2.2. – Amplitud
- 2.2. – Periodo
- 2.2. – Desfase
- 2.2.1. – Actividad 02
- 2.3. Cónicas
- 2.3.1. Superficie cónica de revolución
- 2.3.2. Sección cónica
- 2.3.3. Cónicas degeneradas
- 2.3.4. – Actividad 03
- 2.3.5. La circunferencia
- 2.3.5.1. Ecuación canónica de la circunferencia
- 2.3.5.2. – Actividad 04
- 2.3.5.3. Ecuación general de la circunferencia
- 2.3.5.4. Caracterización del la ecuación de la circunferencia
- 2.3.5.5. – Actividad 05
- 2.3.6. La parábola
- 2.3.6.1. Elementos de la parábola
- 2.3.6.2. Ecuaciones canónicas de la parábola
- 2.3.6.3. Determinación de los elementos de la parábola
- 2.3.6.4. – Actividad 06
- 2.3.6.5. Ecuación general de la parábola
- 2.3.6.6. – Actividad 07
- 2.4. Conteo y probabilidad
- 2.4. – Diagrama de árbol
- 2.4. – Combinaciones
- 2.4. – Permutaciones
- 2.4.1. – Actividad 08
- 2.4.2. Aplicaciones de las técnicas de conteo en la probabilidad
- 2.4.3. – Actividad 09
- 2.5. Probabilidad condicional
- 2.5.1. – Actividad 10
- 3. Bibliografía y webgrafía
2. Funciones Trigonométricas, circunferencia y parábola, probabilidad con conteo y probabilidad condicional
- Un ejemplo de utilización de funciones trigonométricas común es cuando se va al mercado o a cualquier centro comercio donde siempre se relacionan un conjunto de determinados objetos con el costo expresado en pesos para saber cuánto podemos comprar.
- Si lo llevamos al plano, podemos escribir esta correspondencia en una ecuación de función “x” como la cantidad y el precio como “y”, es decir la cantidad en el eje de las abscisas y el precio en el eje de las ordenadas y así expresarlo en un gráfico como el siguiente, donde se expresa que: un Kilogramo de manzana cuesta $3,0
- Entonces: un Kilogramo y medio de manzana cuesta $4,50 etc.
- En la gráfica lo podemos expresar así:
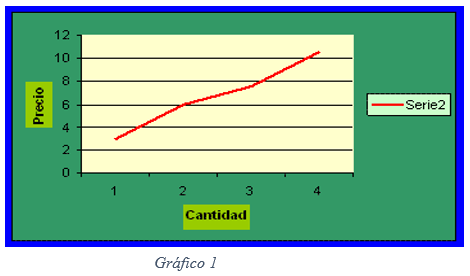
-
- ¿Qué otra información puedo obtener a través de esta gráfica?
- ¿Qué función trigonométrica fue usada?



