MÓDULO II MATEMÁTICAS
- 1. Competencias y Criterios
- 2. Funciones Trigonométricas, circunferencia y parábola, probabilidad con conteo y probabilidad condicional
- 2.1. Funciones Trigonométricas
- 2.1 – Construcción de la tabla de valores
- 2.1 – Análisis de la tabla de valores
- 2.1.1. – Actividad 01
- 2.2. Análisis de gráficas
- 2.2. – Traslaciones de funciones
- 2.2. – Reflexión de funciones
- 2.2. – Compresión y alargamiento
- 2.2. – Amplitud
- 2.2. – Periodo
- 2.2. – Desfase
- 2.2.1. – Actividad 02
- 2.3. Cónicas
- 2.3.1. Superficie cónica de revolución
- 2.3.2. Sección cónica
- 2.3.3. Cónicas degeneradas
- 2.3.4. – Actividad 03
- 2.3.5. La circunferencia
- 2.3.5.1. Ecuación canónica de la circunferencia
- 2.3.5.2. – Actividad 04
- 2.3.5.3. Ecuación general de la circunferencia
- 2.3.5.4. Caracterización del la ecuación de la circunferencia
- 2.3.5.5. – Actividad 05
- 2.3.6. La parábola
- 2.3.6.1. Elementos de la parábola
- 2.3.6.2. Ecuaciones canónicas de la parábola
- 2.3.6.3. Determinación de los elementos de la parábola
- 2.3.6.4. – Actividad 06
- 2.3.6.5. Ecuación general de la parábola
- 2.3.6.6. – Actividad 07
- 2.4. Conteo y probabilidad
- 2.4. – Diagrama de árbol
- 2.4. – Combinaciones
- 2.4. – Permutaciones
- 2.4.1. – Actividad 08
- 2.4.2. Aplicaciones de las técnicas de conteo en la probabilidad
- 2.4.3. – Actividad 09
- 2.5. Probabilidad condicional
- 2.5.1. – Actividad 10
- 3. Bibliografía y webgrafía
2. Funciones Trigonométricas, circunferencia y parábola, probabilidad con conteo y probabilidad condicional
2.3. Cónicas
2.3.6. La parábola
2.3.6.5. Ecuación general de la parábola - Ejemplo 2
- La trayectoria que describe una pelota de golf al ser lanzada (sin considerar la fricción del aire) está dada por la expresión
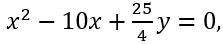 donde x e y se expresa en metros. Hallar la altura máxima que alcanza la pelota y el máximo alcance horizontal.
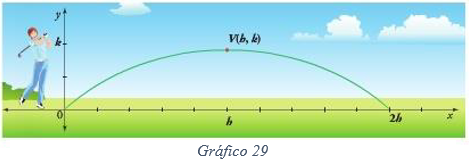
donde x e y se expresa en metros. Hallar la altura máxima que alcanza la pelota y el máximo alcance horizontal. - La ecuación se corresponde con una parábola cuyo eje de simetría es paralelo al eje y. Así, la altura máxima de la parábola corresponde a la coordenada k del vértice V(h, k) de la parábola y el alcance máximo es 2h como se muestra en la siguiente figura.
![]()
- Completo el cuadrado:
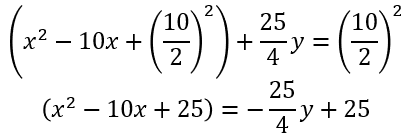
- Factorizo:
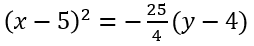
- Entonces V(5, 4), por tanto, la altura máxima que alcanza la pelota es 4 metros y su máximo alcance horizontal es de 2h = 2(5) = 10 metros.



