MÓDULO II MATEMÁTICAS
- 1. Competencias y Criterios
- 2. Los límites y derivadas, la elipse hipérbola y la distribución binominal
- 2.1. Límite de una función
- 2.1.1. – Actividad 01
- 2.2. Límites laterales
- 2.2.1. – Actividad 02
- 2.3. Cálculo de límites
- 2.3.1. Propiedades de los límites
- 2.3.2. – Actividad 03
- 2.4. Límites de funciones indeterminadas
- 2.4.1. Límites de funciones racionales
- 2.4.2. Límites de funciones radicales
- 2.4.3. – Actividad 04
- 2.5. Límites infinitos
- 2.5.1. Límites en el infinito
- 2.5.2. Límites en el infinito de una función racional
- 2.5.3. – Actividad 05
- 2.6. Funciones continuas
- 2.6.1. Funciones continuas evaluados en un punto
- 2.6.2. Funciones continuas evaluados en un intervalo
- 2.6.3. – Actividad 06
- 2.7. Derivada de una función
- 2.7.1. Definición de la derivada de una función
- 2.7.2. Reglas básicas
- 2.7.3. – Actividad 07
- 2.7.4. Recta tangente
- 2.7.5. Recta Normal
- 2.7.6. – Actividad 08
- 2.8. Cónicas
- 2.8.1. Elipse
- 2.8.1.1. Elementos de una elipse.
- 2.8.1.2. Ecuaciones canónicas de la elipse con centro C(0,0)
- 2.8.1.3. Lado recto y excentricidad de una elipse
- 2.8.1.4. – Actividad 09
- 2.8.1.5. Ecuaciones canónicas de la elipse con centro 𝑪 (𝒉,𝒌)
- 2.8.1.6. – Actividad 10
- 2.8.2. La hipérbola
- 2.8.2.1. Elementos de la hipérbola
- 2.8.2.2. Ecuación canónica de la hipérbola con centro (0,0)
- 2.8.2.3. – Actividad 11
- 2.8.2.4. Ecuación canónica de la hipérbola con centro (h,k)
- 2.8.2.5. – Actividad 12
- 2.9. Distribución binominal
- 2.9.1. Propiedades de la distribución binominal
- 2.9.2. Función de distribución nominal
- 2.9.3. – Actividad 13
- 2.9.4. Uso de tablas de probabilidad pronominal
- 2.9.5. – Actividad 14
- 2.10. Valor esperado y varianza
- 2.10.1. – Actividad 15
- 3. Bibliografía y webgrafía
2. Los límites y derivadas, la elipse hipérbola y la distribución binominal
2.8. Cónicas
2.8.1. Elipse
2.8.1.3. Lado recto y excentricidad de una elipse - Ejemplo
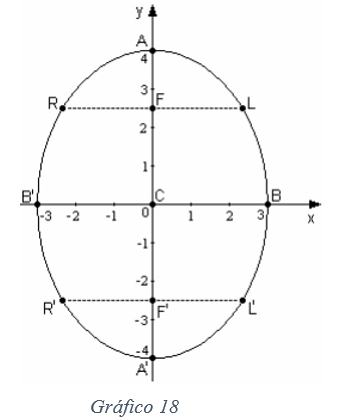
- Bosquejar la gráfica de la elipse
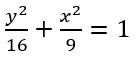
- Para bosquejar la gráfica de la ecuación de la ecuación de la elipse dada, es necesario obtener sus elementos, sabiendo que se trata de una elipse con centro en el origen c(0,0) y eje mayor coincidiendo con el eje y.